Problem
问题描述
给定一个公司的网络,由 n 台交换机和 m 台终端电脑组成,交换机与交换机、交换机与电脑之间使用网络连接。交换机按层级设置,编号为 1 的交换机为根交换机,层级为 1。其他的交换机都连接到一台比自己上一层的交换机上,其层级为对应交换机的层级加 1。所有的终端电脑都直接连接到交换机上。
当信息在电脑、交换机之间传递时,每一步只能通过自己传递到自己所连接的另一台电脑或交换机。请问,电脑与电脑之间传递消息、或者电脑与交换机之间传递消息、或者交换机与交换机之间传递消息最多需要多少步。
样例
输入格式
输入的第一行包含两个整数 n, m,分别表示交换机的台数和终端电脑的台数。
第二行包含 n - 1 个整数,分别表示第2、3、……、 n 台交换机所连接的比自己上一层的交换机的编号。第 i 台交换机所连接的上一层的交换机编号一定比自己的编号小。
第三行包含 m 个整数,分别表示第 1、2、……、m 台终端电脑所连接的交换机的编号。
输出格式
输出一个整数,表示消息传递最多需要的步数。
样例输入
4 2 1 1 3 2 1
样例输出
4
样例说明
样例的网络连接模式如下,其中圆圈表示交换机,方框表示电脑:
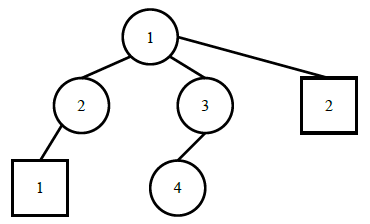 其中电脑1与交换机4之间的消息传递花费的时间最长,为4个单位时间。
其中电脑1与交换机4之间的消息传递花费的时间最长,为4个单位时间。
样例输入
4 4
1 2 2
3 4 4 4
样例输出
4
样例说明
样例的网络连接模式如下:
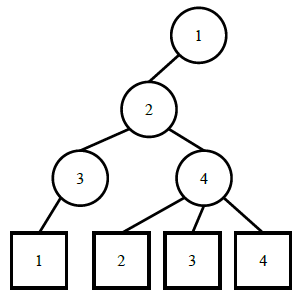 其中电脑1与电脑4之间的消息传递花费的时间最长,为4个单位时间。
其中电脑1与电脑4之间的消息传递花费的时间最长,为4个单位时间。
评测用例规模与约定
前30%的评测用例满足:n ≤ 5, m ≤ 5。
前50%的评测用例满足:n ≤ 20, m ≤ 20。
前70%的评测用例满足:n ≤ 100, m ≤ 100。
所有评测用例都满足:1 ≤ n ≤ 10000,1 ≤ m ≤ 10000。
Solution
问题的本质比较简单,就是求树中任意两个叶子节点的最大路径。求单一个节点的最大路径,可以使用 DFS 或者 BFS 暴搜,于是马上想到了一个版本,对所有的叶子节点 DFS,分别求出其最大路径,然后取其中的最大值。
Version 1
明确了直接暴力 DFS 的方法后,接下来的任务就是读取数据创建数据结构。看到题面给出的图示,很明显可以看到这里描述的是一个树结构,然后想当然地就建立了树节点,构建树结构。读取数据,建立相应的树节点,并将其添加到相应的父节点下。
| |
核心的 DFS 思路为对于当前节点,如果访问过直接退出,否则判断其是否叶子节点,是则结算路径长度,若大于最大路径,则更新。不是叶子节点,则往下递归搜索其子节点。搜完后再往上搜父节点。代码如下:
| |
接下来则主要根据读取的数据确定哪些是叶子节点,然后从叶子节点开始dfs即可,最终提交得分40分,显示运行错误。个人猜测可能是爆了递归空间(然而规模还在40个点内,存疑)。
Version 2
上网搜了一下这个题,发现了一个新的概念——树的直径。树的直径定义为树中两个叶子节点的最大距离,其实也就是我们题目中所求的东西。对于树的直径,可以有一个比较简单的方法计算:
- 从任意一个节点 s 开始,通过 DFS 或者 BFS 找出该节点的最长路径以及路径另一端的节点u
- 从 1 求出的节点 u 开始 DFS 或者 BFS 找出最长路径 u-t,这个最长路径则为整个树中的任意两节点的最长路径
这方法很好证明,在第一步中,我们任意一个节点 s 开始的 DFS 找到的最长路径的另一端节点u必然是最长路径的一个端点,因为
- 若s在最长路径上,搜索结果必然是最长路径的端点
- 若s不在最长路径上,使用反证法,可分为
- 最长路径与2结果有交点
- 最长路径与2结果无交点
因此,根据上述的方法引入,直接可以修改版本1的代码,在dfs函数中,添加对最长路径端点的记录,即可将dfs的规模降低至只需两次dfs,再次提交,只有60分,也是显示运行错误,郁闷。
Version 3
因为此前提示的都是运行错误而不是超时,考虑可能是超出递归的空间限制,睡醒后决定重新写一个BFS的版本。在上午查阅别人代码时,发现大家都是直接用图来表示树结构,仔细想了一下,确实是可以的
- 首先,树就是一个无向图
- 其次,在求最大路径长度时,其实是不需要考虑它判断它是否叶子节点,如果路径的端点不是叶子,则一定其子节点的路径长度一定比它大
- 另外,题目给出的是交换机和计算机,看上去有区别,我在第一个版本也将其分开了,但是其实两个都还是一样的节点,并不需要区别
然后原理还是利用版本2中求两次最大长度的方法,不过这一次我选择使用BFS,用队列循环代替递归,防止运行错误。核心BFS代码如下:
| |
重新提交后,获得100分,用时也比上面的短。